DTMF con algoritmo de Goertzel en ADSP-2181

Código fuente y artículo original en https://github.com/metalamin/DSP-Goertzel

El cálculo de todos los valor de la DFT no es necesario a la hora de implementar un detector DTMF, entonces hacer la FFT puede suponer un peso computacional innecesario y mejorable. Por esa razón se hace uso del Algoritmo de Goertzel que permite calcular la DFT únicamente en las frecuencias deseadas para comprobar la presencia del par de tonos que corresponden al número marcado.

En este trabajo se pretende implementar el citado Algoritmo de Goertzel que permite calcular un valor de X[k] mediante ﬁltrado.

El objetivo es de obtener un detector funcional de marcación DTMF con una salida visual por el osciloscopio. La implementación se hace sobre la placa de desarrollo EZKIT-Lite de Analog Devices basada en el ADSP-2181 del mismo fabricante.

El algoritmo consiste en 2 partes: Una recursiva mientras se reciben datos, y la segunda que se hace cada N muestras para calcular el resultado de la DFT.

En pseudo código tenemos que implementar lo siguiente:

s_prev = 0;
s_prev2 = 0;
normalized_frequency = target_frequency / sample_rate;
coeff = 2 * cos (2* PI* normalized_frequency );
for each sample , x [ n ] , 
	s = x [ n ] + coeff ∗ s_prev − s_prev2 ; 
	s_prev2 = s_prev ; 
	s_prev = s ;
end 
power = s_prev2 ∗ s_prev2 + s_prev ∗ s_prev − coeff ∗ s_prev ∗ s_prev2 

Vemos que la segunda parte es un poco diferente ya que es una manera “optimizada” de obtener el resultado.

$magnitude^2= Q_1^2+Q_2^2-Q_1*Q_2*coef$

Trabajo previo

Para poder implementar el algoritmo de Goertzel en el DSP necesitamos calcular una serie de valores.

Valor de N

N corresponde al numero de muestras que se hacen en la parte recursiva antes de hacer el cálculo ﬁnal del valor de la DFT. Fijamos una resolución del análisis espectral a 10Hz y haremos el calculo partiendo de este requerimiento.

Siendo k los diferentes coeﬁcientes en los que se puede calcular la DFT. Tenemos:

$\frac{f_{tono}}{k}=\frac{f_s}{N}$

Calculamos N para que el cambio de una unidad de k corresponda a 10Hz.

$N=\frac{f_s}{f_{tono}}=\frac{8000}{10}=800$

Escalado de la señal de entrada

Para evitar saturación del ﬁltro necesitamos hacer un escalado de la señal de entrada.

Después de hacer el análisis con tonos a la entrada, vemos que no es la manera correcta ya que saturaba. Eso es debido al sumatorio resultante de la parte recursiva cuyo valor máximo es el sumatorio de N valores cuyo valor absoluto máximo es 1. Como el valor de entrada del DSP esta normalizado entre -1 y 1, tendremos que hacer un escalado de 1/800.

El valor a utilizar en el DSP es: $ganancia=\frac{1}{800}*2^{15}=40.96$

Por lo tanto hay que realizar un escalado en el DSP de 40. De esta manera se evitar la saturación.

Valores de los coeﬁcientes

Como se pretende detectar los 8 tonos de la tabla DTMF, tendremos que calcular los coeﬁcientes correspondientes.

$Coef=2*cos(2\pi*\frac{f_{tono}}{f_s})$

Para poder guardar los valores en coma ﬁja en el DSP queremos que tengan un valor absoluto inferior a la unidad. Calculamos el valor de coseno solo y ya lo multiplicaremos por 2 a posteriori. A continuación, tenemos la tabla de los coeficientes. (la mitad)

Frecuencia	Coeficiente	Valor en el DSP
697	0,8539	27980
770	0,8226	26956
852	0,7843	25701
941	0,7391	24219
1209	0,5821	19073
1336	0,4982	16325
1477	0,3993	13085
1633	0,2843	9315

Amplitud de detección de tono

El valor del tono detectado tiene que ser superior al 20% de la amplitud máxima de entrada para considerarse positivo. Tenemos que el valor máximo a la entrada es de 40 (en el DSP) por el escalado. Por lo que ﬁjaremos el umbral al 20% de 40 $umbral=40*20/100=8$ Se considerará el tono detectado cuando supere ese umbral.

Programa en MATLAB

Antes de empezar a programar en el DSP se trabaja en MATLAB para veriﬁcar el funcionamiento correcto del algoritmo.

El archivo correspondiente de MATLAB es migoertzel.m e implementa la función:

$y = migoertzel(x)$

El programa primero inicializa los valores y luego ejecuta 2 bucles: Uno para hacer ventanas de 800 muestras y luego el bucle correspondiente a la primera parte del algoritmo. Finalmente calcula el valor ﬁnal para todos los tonos.

No saca el valor del dígito marcado pero se puede apreciar fácilmente en que momentos se supera el umbral de los tonos.

Sea x la señal muestreada a 8000Hz se usa de la siguiente manera:

>> x= sin (2* pi * t *770) ; % 770Hz
>> y= migoertzel (x /800) *2^15; 
>> round (y ) 
ans = 0 8132 0 0 0 0 0 0

Vemos que se ha dividido la señal por N para hacer el escalado que tendríamos que hacer en el DSP. En este ejemplo se aprecia como detecta perfectamente el segundo tono correspondiente a la frecuencia 770 Hz. Si se hace con un tono puro y amplitud máxima de entrada vemos que los valores son son próximos a 8000, superando con varios ordenes de magnitud el umbral.

Probamos a ver si con una frecuencia cercana da un falso positivo.

>> x= sin (2* pi * t *760) ; % 760Hz
>> y= migoertzel (x /800) *2^15; 
>> round (y ) 
ans = 0 0 0 0 0 0 0 0

No se detecta la frecuencia en este caso. Por lo que se comporta como es deseado.

Programa en DSP

Partimos de la simple detección de la marcación del 0 que enciende un led, luego se amplia para detectar los 8 tonos y sacar por el osciloscopio una respuesta que caracteriza cada numero.

Detector de marcación del Cero.

Esta primera parte consigue la detección de 2 tonos correspondientes al ’0’. Para ello implementa el algoritmo de Goertzel con buffer circular para ir haciendo la parte recursiva. Luego se repite el mismo código para cada tono (2 veces).

mx0=dm( i2 ,m2); 
my0=dm( coef1 );	{Cargamos q1 y coef } 
mr=mx0*my0( ss );	{q1* cos ( alpha ) }

my0=1; 
mr=mr1*my0( ss );	{q1 *2* cos ( alpha ) } 
ar=mr0;

mx0 = dm( rx_buf + 1); { input } 
my0=dm( ganancia );
mr=mx0*my0( ss ); 
ay0=mr1; 
ar=ar+ay0;			{ input+q1 *2* cos ( alpha ) } 
ay0=dm( i2 ,m3);	{cargamos q2}

ar=ar−ay0;			{ input+q1 *2* cos ( alpha )−q2} 
dm( i2 ,m3)=ar ;

Si queremos ver si funciona bien sacamos por la pantalla los valores de q1 o de q2 por el osciloscopio cada muestra. Y debería dar algo parecido a la siguiente ﬁgura cuando en la entrada se introduce el tono correspondiente.

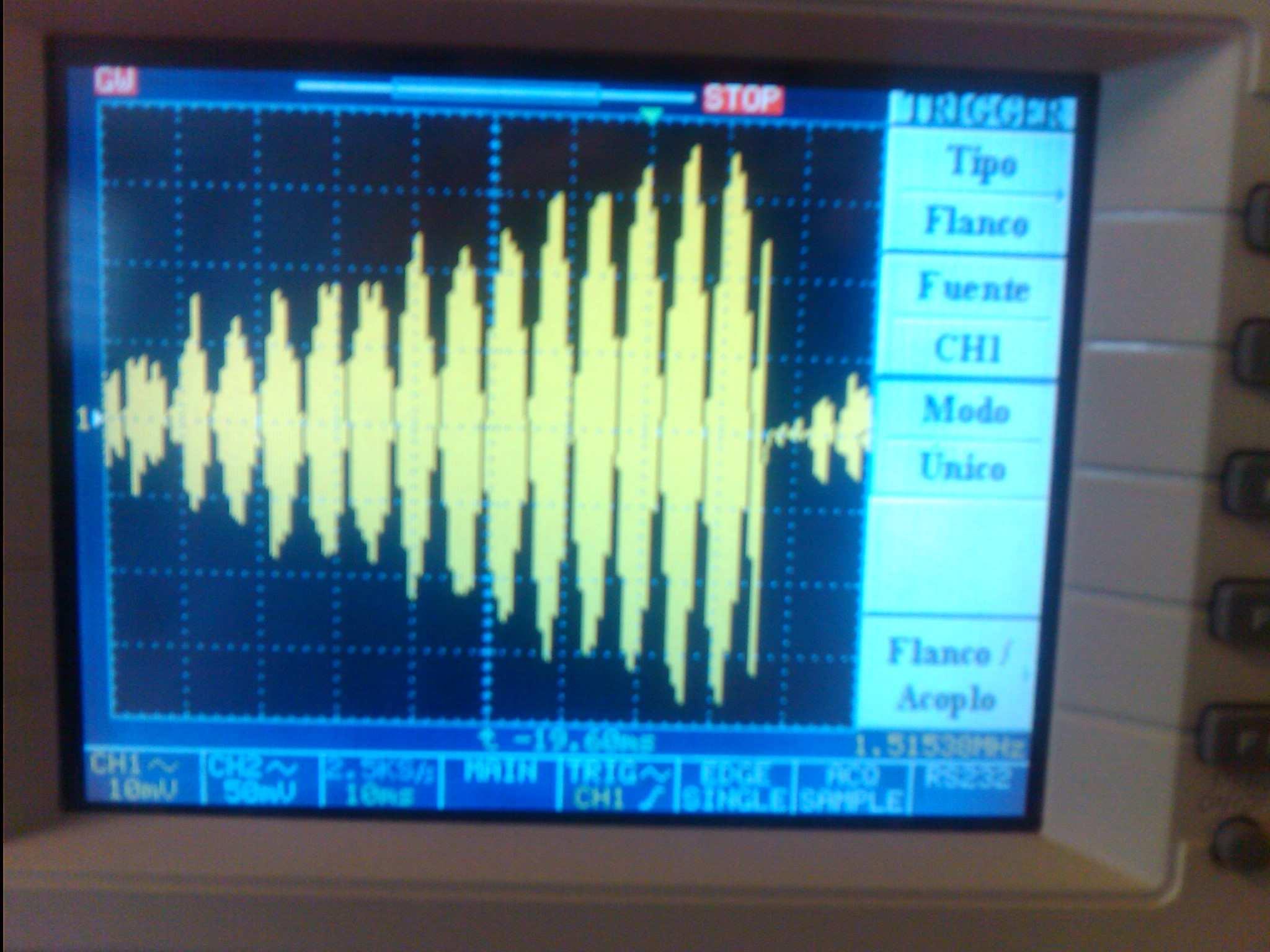
Señal correspondiente a los valores de q1

Vemos que el valor de q1 se va haciendo mas grande hasta llegar a las N muestras. Entonces se usan los valores y se vuelve a reinicializar para dejarlo preparado para la siguiente pasada de N muestras.

Después de N muestras se hace el calculo ﬁnal.

ar=dm( coef1 ); 
my0=1; mr=ar *my0( ss ); 
ar=mr0;				{ coef * 2}

mx0=dm( i2 ,m2);	{Obtener q1 dos veces} 
my0=mx0; 
mx1=dm( i2 ,m2);	{Obtener q2 dos veces} 
my1=mx1;
mr=0; mf=mx0*my1( ss );	{q1*q2} 
mr=mr − ar ∗mf( ss );	{−q1*q2* coef} 
mr=mr+mx0*my0( ss );	{q1^1−q1*q2* coef}
mr=mr+mx1*my1( ss );	{q2^2+q1^2−q1*q2* coef} 
dm( sqr1 )=mr1;

Comparar con el umbral y encender el LED. Finalmente hay que reinicializar a 0 los valores.

salida:
	ay0=dm( umbral );
	ax0=dm( sqr1 );
	ar=ax0 − ay0 ; 
	if lt jump apagado; 
	ax0=dm( sqr2 );
	ar=ax0 − ay0; 
	if lt jump apagado; 
	set fl1;
	rts;
apagado :
	reset fl1; 
	rts;

Decodificador DTMF

El archivo ’goertzel.dsp’ consigue decodiﬁcar la marcación telefónica mediante la detección de 8 tonos correspondientes a la tabla DTMF . Para ello implementa el algoritmo de Goertzel sin el buffer circular pues necesita guardar 16 valores de q. Es posible implementarlo con buffers circulares pero la complejidad ha impedido que se pueda hacer en poco tiempo.

Se ha modiﬁcado el programa anterior para hacer los cálculos de los valores intermedios a cada muestra en un bucle para rellenar los 16 valores del vector.

cntr=tonos; 				{Repetimos para cada tono}
do parte1 until ce;
	mx0=dm(i2,m1);
	my0=dm(i5,m4);			{Cargamos q1 y coeficiente}
	mr=mx0*my0(ss), ay0=dm(i2,m3);
							{q1*coef, obtener q2}
	my0=1;
	mr=mr1*my0(ss); 		{q1*2*cos(alpha)}
	ar=mr0-ay0;				{q1*2*coef - q2}
	ar=ar+ay1;				{q1*2*coef - q2 + entrada}
	dm(i2,m1)=ar;			{suma -> q1}
parte1: dm(i2,m1)=mx0;		{q1 -> q2}

Vemos que en este caso el código es mejorable pues en cada pasada mueve de sitio los valores en la memoria.

Luego se calculan los valores ﬁnales de la misma manera que el programa anterior y se guardan en un vector.

Finalmente para decodiﬁcar el número correspondiente, se hace mediante una serie de condiciones. Se ha obviado el caso de las combinaciones que no corresponden a números para facilitar la diferenciación en el osciloscopio.

salida:
	ay0=dm(umbral);
	mx0=0;
	
	ax0=dm(sqr);
	ar=ax0 - ay0;
	if ge jump fila0;
	ax0=dm(sqr+1);
	ar=ax0 - ay0;
	if ge jump fila1;
	ax0=dm(sqr+2);
	ar=ax0 - ay0;
	if ge jump fila2;
	ax0=dm(sqr+3);
	ar=ax0 - ay0;
	if ge jump fila3;
	mx0=0;
	jump sacaresul;
	rts;
	
fila0:
	ax0=dm(sqr+4);
	ar=ax0 - ay0;
	mx0=6400;						{Nivel a sacar para '1'}
	if ge jump sacaresul;
	ax0=dm(sqr+5);
	ar=ax0 - ay0;
	mx0=9600;						{Nivel a sacar para '2'}
	if ge jump sacaresul;
	ax0=dm(sqr+6);
	ar=ax0 - ay0;
	mx0=12800;						{Nivel a sacar para '3'}
	if ge jump sacaresul;
	ax0=dm(sqr+7);
	ar=ax0 - ay0;
	mx0=0;
	if ge jump sacaresul;
	
	mx0=0;
	jump sacaresul;
....

....
sacaresul:
	dm(cambia)=mx0;
	rts;

Problemas encontrados

No se puede hacer debug y ver los valores intermedios. Aunque tenemos algunos métodos de feedback que consisten en un led y la salida analógica. Pero la salida no puede ser constante por lo que hay que hacer pequeños ’hacks’ para saltar esta limitación. El truco consiste en alternar el valor entre positivo y negativo para evitar la continua.

En caso de que deseamos más velocidad, podemos usar una velocidad de muestreo de 48kHz y multiplicar los tonos buscados por 6.

El primer problema encontrado fue al escalar de manera errónea la entrada, entonces siempre se obtienen datos que parecen aleatorios cerca de el tono buscado. Sólo al alejarse lo suﬁciente se obtenía una respuesta nula. Fue debido al cálculo del escalado necesario tomando la primera parte como un ﬁltro normal.

Luego durante alguna modiﬁcación se declaró de manera errónea una variable en el espacio de programa pero se cargaba esa variable desde la memoria de datos. Por lo visto el compilador no se queja ni avisa de este desliz.

Finalmente, al usar el puntero i3 el programa se colgaba de manera que había que apagar el DSP para poder reinicializarlo. Eso es porque el programa base ya usa ese puntero y hay que evitar reutilizarlo.

Resultado

Se ha hecho la prueba con tonos desde el generador de de señales usando una modulación AM para emular los dos tonos y luego conectando la entrada a la salida audio del PC. El detector de DTMF funciona, incluso al bajar el volumen y con música reproduciéndose al mismo tiempo.

Para ver la salida en el osciloscopio se ha puesto el nivel de GND en la parte baja de la pantalla de manera que si no se detecta ningún numero no se vea nada.

Luego a cada número, del 0 al 9, corresponde un nivel de manera creciente. Aprovechamos toda la pantalla des oscilloscopio para diferenciar fácilmente los números. Vemos unos ejemplos:

Salida correspondiente a ’Nada Detectado’

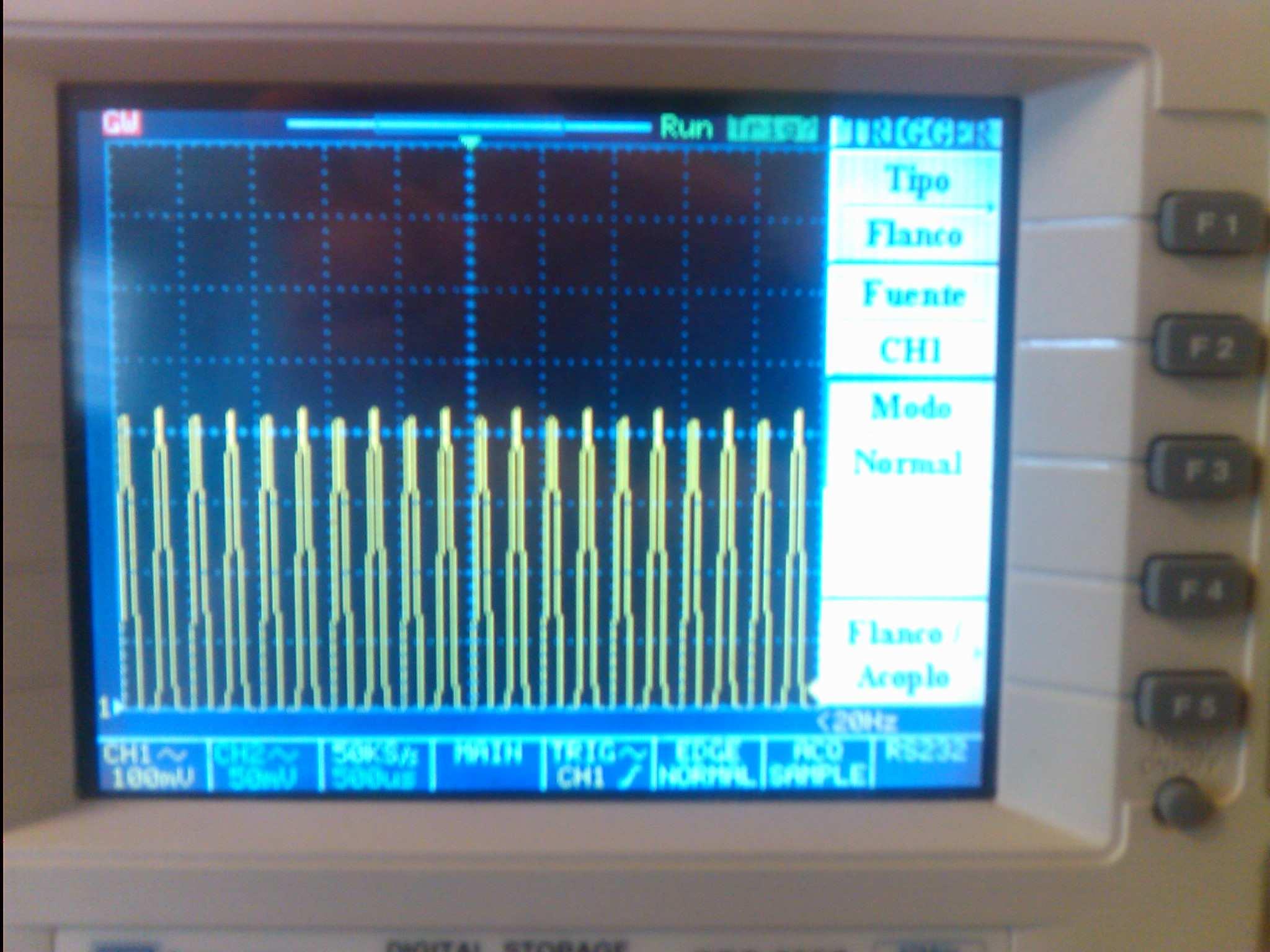
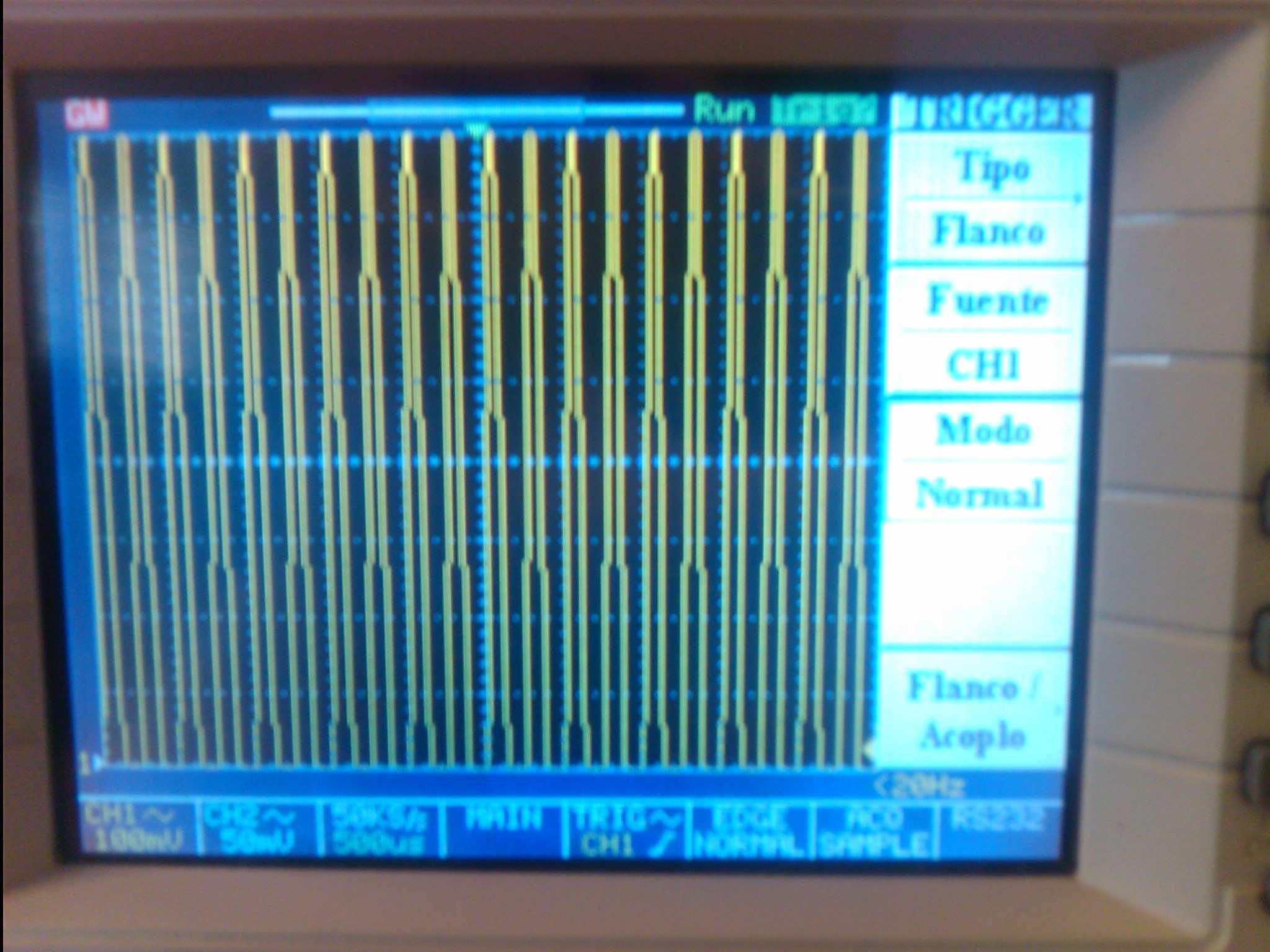
Posibles mejoras

El código no esta optimizado, se puede mejorar haciendo uso de memoria de programa y de datos de manera alterna, luego haciendo uso de buffers circulares.

Podemos incluir detección de tonos erróneos (2 tonos columna o 2 tonos ﬁla) para encender el LED como error y mejorar el algoritmo de decodiﬁcación del numero

Twitter Facebook Google+ LinkedIn

Amine Taouirsa